개요와 목적
코딩 테스트 대표적인 자바 투포인터 문제들을 풀어보고,
배열의 문제 풀이 방식에 대해서 알아본다.
두 배열 합치기

3 1 3 5 5 2 3 6 7 9
풀이
두 배열 index 0부터 서로 비교한다. 더 작은 쪽을 answer에 추가하고, 인덱스를 한 칸 올려, 다음 수를 비교 대상으로 정한다.
이런 식으로 반복하여, answer를 만든다.
import java.util.ArrayList;
import java.util.Scanner;
public class 두배열합치기 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
int m = sc.nextInt();
int[] b = new int[m];
for (int i = 0; i < m; i++) {
b[i] = sc.nextInt();
}
ArrayList<Integer> answer = new ArrayList<>();
int p1=0, p2=0;
while(p1<n && p2<m){
if (a[p1] < b[p2]) {
answer.add(a[p1]);
p1++;
} else {
answer.add(b[p2]);
p2++;
}
}
while (p1 < n) {
answer.add(a[p1]);
p1++;
}
while (p2 < m) {
answer.add(b[p2]);
p2++;
}
System.out.println(answer);
}
}
공통 원소 구하기

5 1 3 9 5 2 5 3 2 5 7 8
풀이
위 두배열 합치기 풀이와 같은 방식으로 풀면된다.
public class 공통원소구하기 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] a = new int[n];
for(int i=0; i<n; i++){
a[i]=sc.nextInt();
}
int m=sc.nextInt();
int[] b=new int[m];
for(int i=0; i<m; i++){
b[i]=sc.nextInt();
}
ArrayList<Integer> answer = new ArrayList<>();
//먼저 주어진 배열을 오름 차순으로 정렬한다.
Arrays.sort(a);
Arrays.sort(b);
int p1 = 0, p2 = 0;
while (p1 < n && p2 < m) {
//a 기준으로 b의 값이 같으면,
//값을 추가한다음 a,b와 인덱스 동시에 올려준다
if (a[p1] == b[p2]) {
answer.add(a[p1++]);
p2++;
//b의 값이 크다면 a 인덱스만 올려준다.
} else if (a[p1] < b[p2]) {
p1++;
//a의 값이 크다면 b 인덱스만 올려준다.
} else {
p2++;
}
}
System.out.println(answer);
}
}
연속 부분 수열

8 6 1 2 1 3 1 1 1 2
풀이
먼저 배열의 시작 부분 lt와 끝 부분 rt를 정한다. sum은 lt와 rt 안에 있는 배열의 합이다.
합이 목표값(m,6)보다 같거나 작으면 rt++해서 연속 부분수열 범위를 늘린 sum 값을 찾는다.
sum값이 m보다 커지면 같거나 작아질 때까지 기존 lt값을 빼고 lt++해서 부분 수열 범위를 줄인다.

import java.util.Scanner;
public class 연속부분수열 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
System.out.println(solution(n, m, arr));
}
public static int solution(int n, int m, int[] arr) {
int answer = 0, sum = 0, lt = 0;
for (int rt = 0; rt < n; rt++) {
sum += arr[rt];
if (sum == m) {
answer++;
}
while (sum >= m) {
sum -= arr[lt++];
if (sum == m) {
answer++;
}
}
}
return answer;
}
}
연속된 자연수의 합

풀이 1
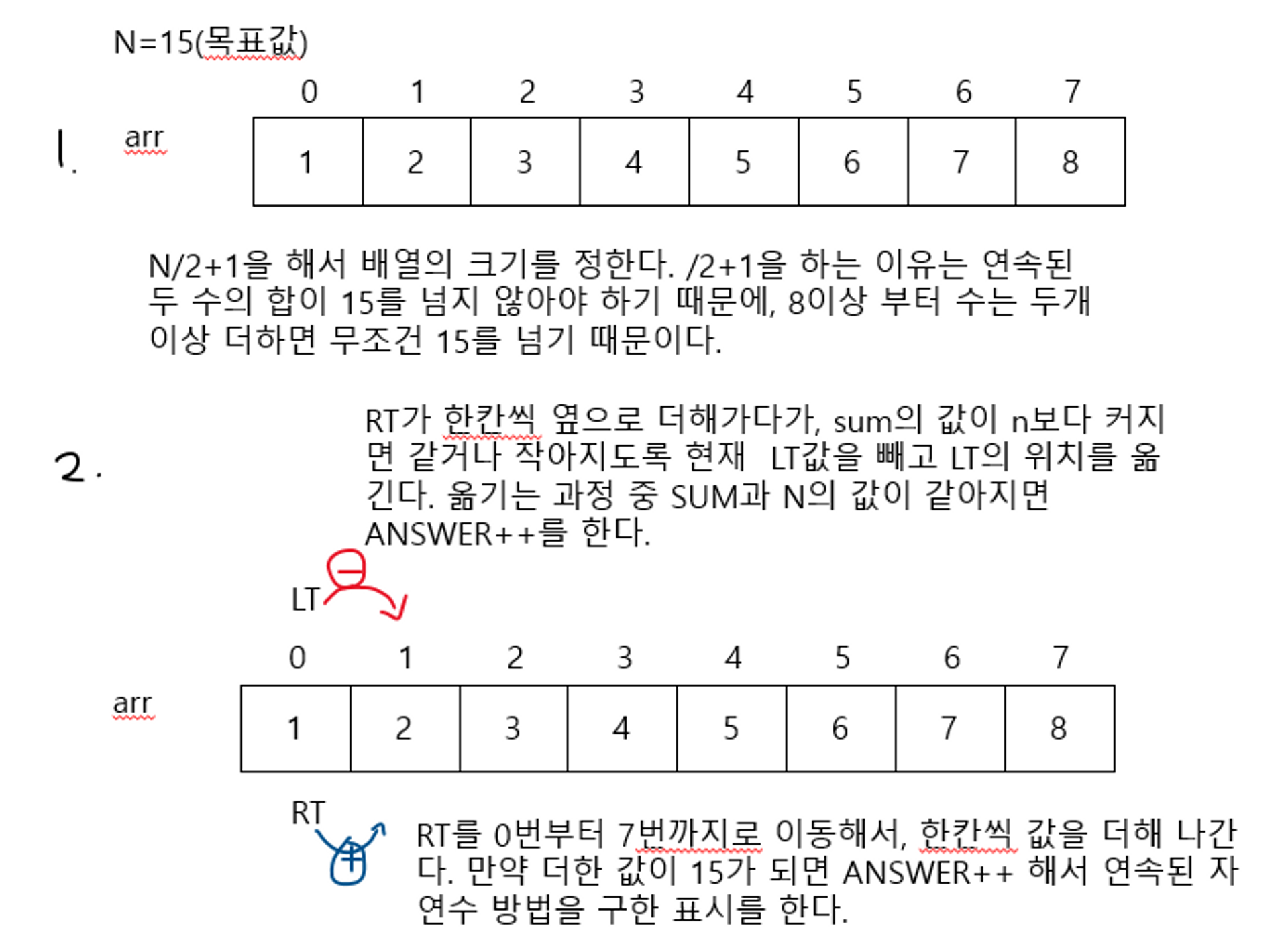
public class 연속된자연수의합 {
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
System.out.print(solution(n));
}
public static int solution(int n) {
int answer = 0, sum = 0;
int m = n / 2 + 1;
int[] arr = new int[m];
for(int i=0; i<m; i++) arr[i]=i+1;
int lt = 0;
for (int rt = 0; rt < m; rt++) {
sum += arr[rt];
if (sum == n) {
answer++;
}
//sum이 목표값보다 크면 lt위치 값을 빼고, lt를 한칸 전진한다.
while (sum >= n) {
sum -= arr[lt++];
if (sum == n) {
answer++;
}
}
}
return answer;
}
}
풀이 2 - 수학적 방법
수학적 지식을 첨가해서 다른 풀이로 풀어보자
아래 방법으로 가능 불가능을 나누어서 가능한 수의 합을 출력하면 된다.

public class 연속된자연수의합수학방법 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int answer = 0;
//풀이
int m = n / 2 + 1;
for (int i = 2; i <= m; i++) {
int temp = n;
// 2개부터 8개까지 쪼개지는 지 확인하기
for (int j = 1; j <= i; j++) {
temp -= j;
}
if (temp>=0 &&temp % i == 0) {
System.out.println(i);
answer++;
}
}
System.out.println(answer);
}
}
최대 길이 연속 부분수열

14 2 1 1 0 0 1 1 0 1 1 0 1 1 0 1
풀이
이 문제도 투포인터로 풀면 O(N) 시간 복잡도로 풀 수 있다.

public class 최대길이연속부분수열 {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int k = sc.nextInt();
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
int answer = solution(n, k, arr);
System.out.println(answer);
}
static int solution(int n, int k, int[] arr) {
//cnt는 0을 1로 바꾼 수 k보다 커지면,
// lt가 0을 만날 때까지 lt를 앞으로 옮긴다
int answer = 0, cnt = 0, lt = 0;
//rt가 0부터 끝까지 전진
for (int rt = 0; rt < n; rt++) {
//가는 도중에 0을 만나면 1로 바꾼다고 생각하고 cnt++를 한다.
if (arr[rt] == 0) {
cnt++;
}
while (cnt > k) {
if (arr[lt] == 0) {
cnt--;
}
//lt위치가 0일 때까지 찾는다!!
lt++;
}
answer = Math.max(answer, rt - lt + 1);
}
return answer;
}
}
'자바 자료구조 알고리즘 > 문자열 & 배열 & 투포인터 & 정렬' 카테고리의 다른 글
| 코딩 테스트 Java 정렬 문제 풀이 (0) | 2023.05.06 |
|---|---|
| 코딩 테스트 Java 배열 문제 풀이 (0) | 2023.05.02 |
| 코딩 테스트 Java 문자열 문제 풀이 (0) | 2023.04.24 |


