개요 목적
Java DFS 기초 이해와 문제 풀이 해당 글에서는 재귀함수와 DFS 기초를 알아보았다.
이번 시간에는 DFS 활용 문제를 풀면서 DFS 문제 풀이 실력을 늘려보자.
합이 같은 부분집합(DFS : 아마존 인터뷰)

6 1 3 5 6 7 10
풀이1. ch 배열( 해당 숫자 포함될 때, 안될 때 - 사용)
import java.util.*;
class Main {
static int n;
static int[] arr;
static int[] ch;
static int half;
static boolean result;
public void DFS(int v) {
if (v == n+1) {
System.out.println(Arrays.toString(ch));
int sum = 0;
for (int i = 1; i < ch.length; i++) {
if (ch[i] == 1) {
sum += arr[i];
}
}
if (sum == half) {
result = true;
}
} else {
ch[v] = 1;
DFS(v + 1);
ch[v] = 0;
DFS(v + 1);
}
}
public static void main(String[] args){
result = false;
Main T = new Main();
Scanner kb = new Scanner(System.in);
n=kb.nextInt();
arr = new int[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = kb.nextInt();
}
ch = new int[n + 1];
half = Arrays.stream(arr).sum() / 2;
//[1,3,5,6,7,10]
T.DFS(1);
}
}
ch 배열에 각 인덱스 번호가 집합[1,3,5,6,7,10]을 의미한다. 예를 들어 ch[1] =1 ch[2] =3 ch[6] =10이다. ch의 0번 인덱스는 편의를 위해 사용하지 않는다.
재귀 함수 DFS를 돌때, ch 1번 인덱스가 포함될 때와 안 될 때를 나눠서 재귀 함수를 돌게 하여 부분집합 경우의 수를 구한다.
자세한 설명은 재귀함수 DFS 기초 글에서 확인 할 수 있다.
풀이 2. 합을 파라미터에 넣어서, 포함된 것과 포함되지 않은 경우의 수 구하기.
public class 합이같은부분집합 {
static String answer = "NO";
static int n, total = 0;
static boolean flag = false;
static int[] arr;
public static void DFS(int L, int sum) {
if (flag) return;
if (L == n) {
if ((total - sum) == sum) {
answer = "YES";
flag = true;
}
} else {
//포함 된 것 arr[L]의 값이 합으로 들어 간 것
DFS(L + 1, sum + arr[L]);
//arr[L]의 값이 합으로 포함되지 않은 경우
DFS(L + 1, sum);
}
}
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
n=kb.nextInt();
arr=new int[n];
for(int i=0; i<n; i++){
arr[i]=kb.nextInt();
total+=arr[i];
}
//[1,3,5,6,7,10]
DFS(0, 0);
System.out.println(answer);
}
}
이번에는 ch배열을 사용하는 것이 아니라, 파리미터 sum 값을 넣어서, 각 숫자가 포함된 경우와 포함되지 않은 재귀 함수를 만들어 부분 집합의 합 경우의 수를 완성한다.
최대 점수 구하기

5 20 10 5 25 12 15 8 6 3 7 4
풀이
import java.util.Scanner;
public class 최대점수구하기 {
static class Node {
int time;
int score;
public Node(int time, int score) {
this.time = time;
this.score = score;
}
}
static int n, m;
static int result = Integer.MIN_VALUE;
static Node[] arr;
//v가 == 5일 때 즉 부분집합의 경우의 수를 완성 했을 때,
// 시간의 합과 점수 합을 비교하기 위해 파라미터에 넣어두었다.
public static void DFS(int v, int timeSum, int scoreSum) {
//DFS를 진행하다가, 시간의 합이 기준보다 초과하면 그 아래 DFS 진행하지 않고 바로 끝내버린다.
if (timeSum > m) {
return;
}
if (v == n) {
result = Integer.max(result, scoreSum);
} else {
//점수10시간5가 포함 되었을 때,
DFS(v + 1, timeSum + arr[v].time, scoreSum + arr[v].score);
//점수10시간5가 포함 되지 않았을 때, 경우의 수
DFS(v + 1, timeSum , scoreSum);
//구할 수 있게 DFS를 설정했다.
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new Node[n];
for (int i = 0; i < arr.length; i++) {
int score = sc.nextInt();
int time = sc.nextInt();
arr[i] = new Node(time, score);
}
DFS(0, 0, 0);
System.out.println(result);
}
}
DFS 파라미터 안에, sum과 time의 넣어 그 값들을 들고 다니면서, 부분 집합의 경우의 수에서 어떤 결과를 내고 있는 지 한번에 파악이 가능하다.
중복 순열 구하기

3 2
풀이
아래와 같은 그림이 만들어 지도록, L(레벨)과 같은 2개의 인덱스를 가진 arr를 만들어서 L레벨 당 DFS에서 값을 넣을 수 있도록 했다.
import java.util.Arrays;
import java.util.Scanner;
public class 중복순열 {
static int n, m;
static int[] arr;
public static void DFS(int L) {
if (L == m) {
System.out.println(Arrays.toString(arr));
} else {
for (int i = 1; i <= n; i++) {
arr[L] = i;
DFS(L + 1);
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new int[m];
DFS(0);
}
}

순열 구하기

3 2 3 6 9
풀이
위 중복 순열과 다른 방식은, 순열에 사용한 숫자들이 들어 있는 arr 배열 인덱스와 같은 ch배열을 생성해서, 중복이 안된 경우에만 DFS에 들어갈 수 있도록 풀이한 것이다.
import java.util.Arrays;
import java.util.Scanner;
public class 순열구하기 {
static int[] pm, ch, arr;
static int n, m;
public static void DFS(int L) {
if (L == m) {
System.out.println(Arrays.toString(ch));
for(int x : pm) System.out.print(x+" ");
System.out.println();
} else {
for (int i = 0; i < n; i++) {
if (ch[i] == 0) {
ch[i] = 1;
pm[L] = arr[i];
DFS(L + 1);
ch[i] = 0;
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n=sc.nextInt();
m=sc.nextInt();
arr=new int[n];
for(int i=0; i<n; i++) arr[i]=sc.nextInt();
//레벨 별 값을 넣을 것이기 때문에 레벨과 같은 2 로 설정한다.
pm = new int[m];
//중복을 허용하지 않게, arr[3,6,9] 인덱스 번호로, pm에 해당 값이 있는 지 체크할 수 있는 배열을 만들어준다
//그래서 숫자를 담아놓은 arr배열과 같은 3으로 설정한다.
ch = new int[n];
DFS(0);
}
}
[1, 1, 0]
3 6
[1, 0, 1]
3 9
[1, 1, 0]
6 3
[0, 1, 1]
6 9
[1, 0, 1]
9 3
[0, 1, 1]
9 6
조합의 수 구하기

5 3
33 19
풀이
먼저 조합과 순열의 차이는, 조합은 뽑는 순서를 고려하지 않는다는 것이다.

그리고 5C3을 = 4C3+4C2으로 나타낼 수 있는데, 왜 이렇게 변형할 수 있는 지 알아보자
{1,2,3,4,5} 가 있는 상황에서 3개를 뽑는 경우를 5번 학생 입장에서 바라본다면,
5번 학생 입장에서 뽑혀서 나머지 2개를 뽑는 경우나, 5번 학생이 빠져서 4개 중에 3개를 뽑는 경우로 나뉠 수 있다. 그래서 이 두 경우를 더하면 5C3을 구할 수 있다.
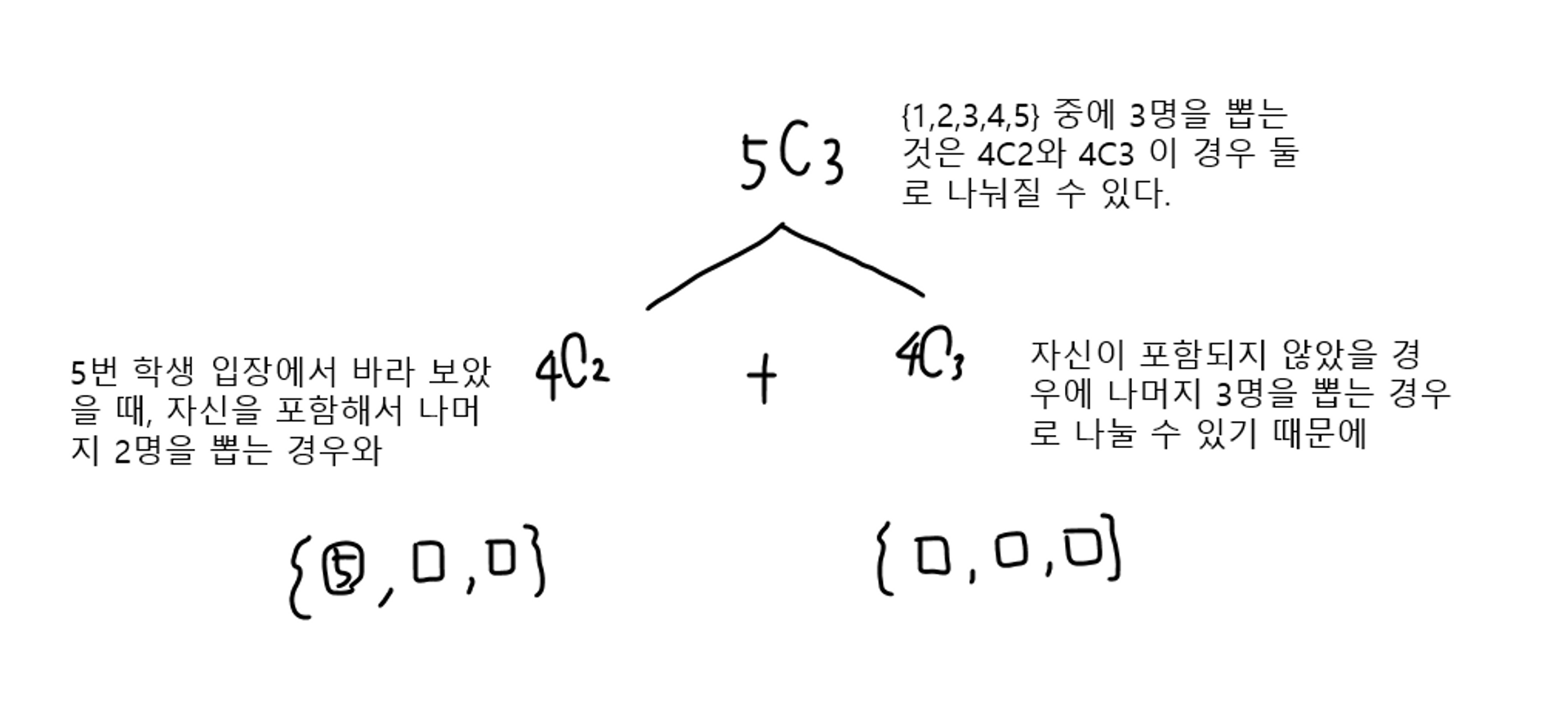
위 조합의 방식을 DFS로 활용하여 5C3의 값을 찾아보자.
위 방식대로 내려가다 보면, r=0인 경우와, n=r인 경우를 만나게 된다.
r=0 일 때는 결과가 무조건 1이다. 예를 들어 2C0(2개 중에 0개를 뽑는 경우는 1개이기 때문)
n=r 일 때도 결과는 무조건 1이다. 예를 들어 3C3 (3개 중에 3개 뽑는 경우는 1개이기 때문)
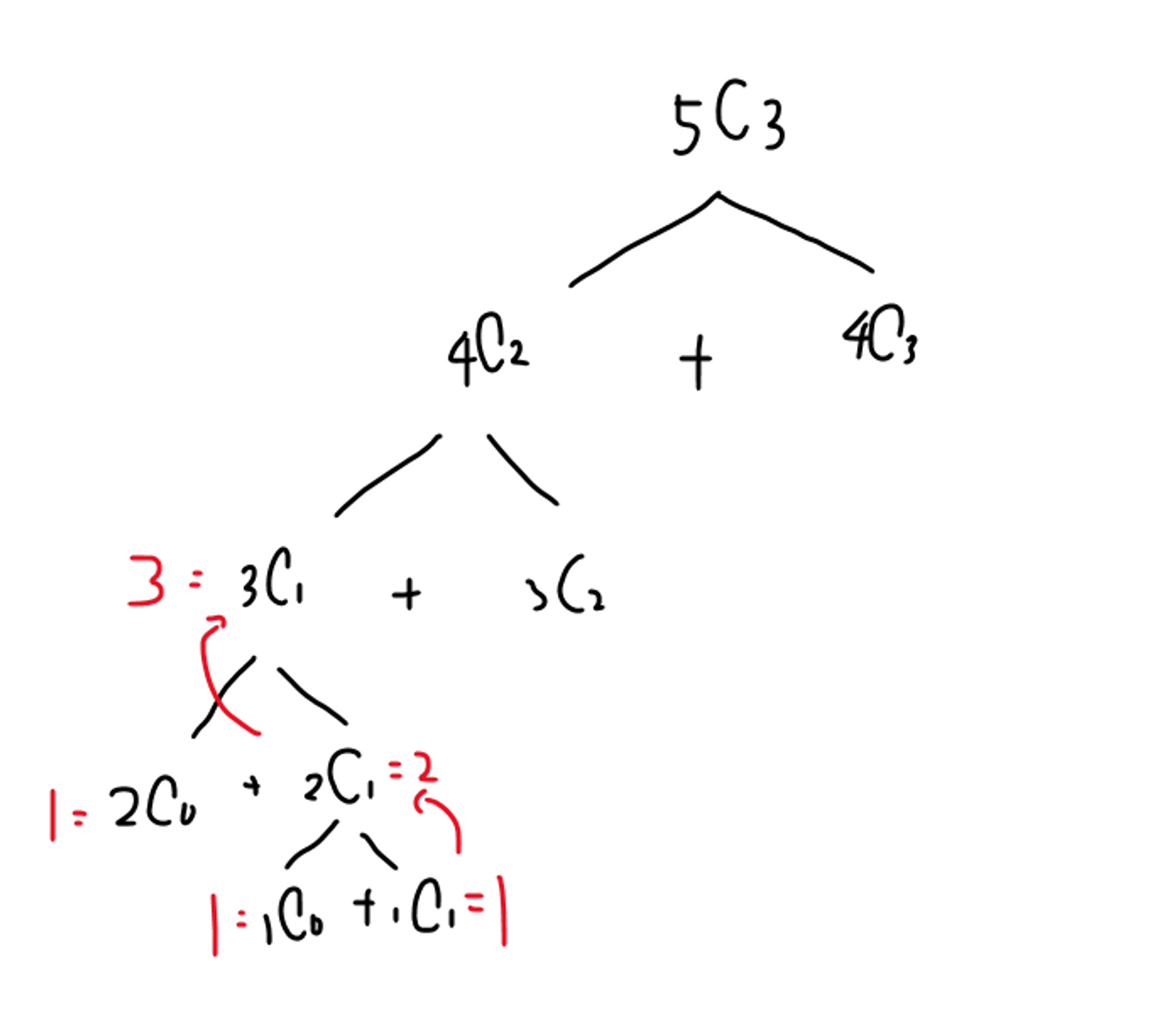
import java.util.Scanner;
public class 조합의경우의수 {
static int[][] dy = new int[35][35];
public static int DFS(int n, int r) {
if (dy[n][r] > 0) {
return dy[n][r];
}
//r=0이거나 n=r이 같은 경우 return 1
if (n == r || r == 0) {
return 1;
} else {
return dy[n][r] = DFS(n - 1, r - 1) + DFS(n - 1, r);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int r = sc.nextInt();
System.out.println(DFS(n,r));
}
}수열 추측하기

4 16
풀이
먼저 3 1 2 4를 아래로 더하지 않고 조합의 수를 사용해서 결과 값을 구하는 방법에 대해서 알아보자.
부분 집합 위치에 따라 첫 번째 수는 3C0번 만큼, 두 번째 수는 3C1, 세 번째 수는 3C2, 네 번째 수는 3C3만큼 곱해져서 더한 값이 16이라는 것을 알 수 있다.
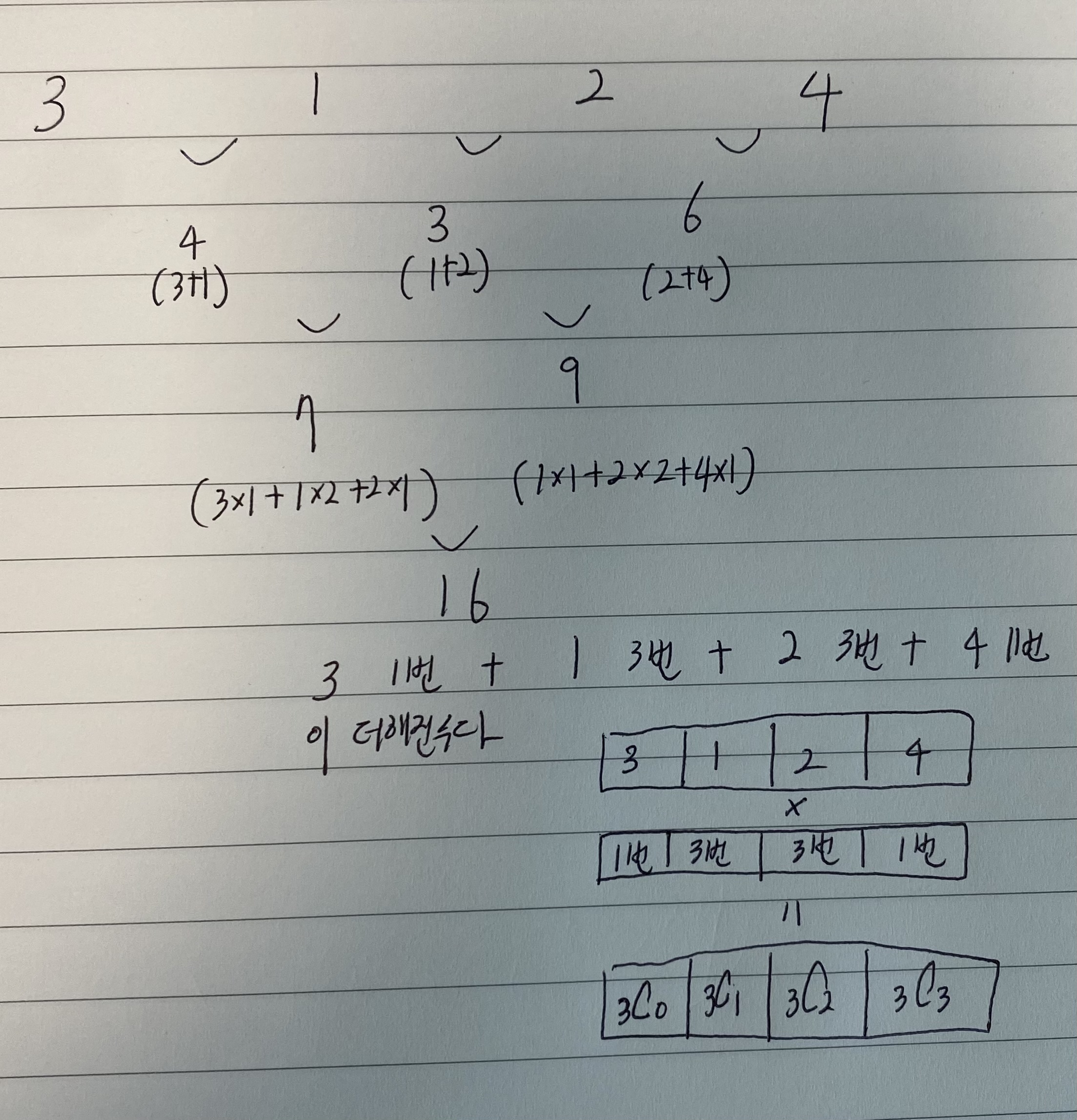
그래서 DFS를 통해 1,2,3,4의 부분 집합을 구하고, 부분 집합 마다 곱해지는 수[3C0, 3C1, 3C2, 3C3]와 곱해서 16이 맞는 지 구하면 이 문제를 풀 수 있다. 코딩으로 자세한 풀이를 알아보자.
import java.util.*;
public class 수열추측하기{
static int n, m;
static int[] comb, p, ch;
static boolean flag = false;
//부분집합 위치마다 곱해지는 조합의 수 구하는 메소드
public static int combi(int n, int r) {
if (n == r || r == 0) {
return 1;
} else {
return combi(n - 1, r) + combi(n - 1, r - 1);
}
}
public static void DFS(int L, int sum) {
if (flag) {
return;
}
if (L == n) {
if (sum == m) {
for(int x : p) System.out.print(x+" ");
flag = true;
}
} else {
for (int i = 1; i <= n; i++) {
if (ch[i] == 0) {
ch[i] = 1;
p[L] = i;
//부분 집합 위치별 조합의 수와 해당 부분집합 위치의 값을 곱해서 sum에 넣어준다.
DFS(L + 1, sum + p[L] * comb[L]);
ch[i] = 0;
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
//m은 목표하는 값
m = sc.nextInt();
comb = new int[n];
for (int i = 0; i < comb.length; i++) {
//3c0 ~ 3c3까지 해당 값 배열에 넣기
comb[i] = combi(n-1, i);
}
//DFS Level 별로 값을 담을 p 배열
p = new int[n];
//중복되지 않는 부분집합을 구하기 위해
ch=new int[n+1];
DFS(0, 0);
}
}
조합 구하기

풀이
수열과 다르게 조합은 순서가 중요하지 않다. 즉 (1,2) 과 (2,1)은 같은 뽑은 종류이기 때문에 (1,2)하나만 사용한다.
조합 같은 경우는 많이 나오기 때문에 식을 그냥 외워버리는 것도 방법이다.
import java.util.Scanner;
public class 조합구하기 {
static int n, r;
//조합을 담을 배열
static int[] combi;
public static void DFS(int L, int s) {
if (L == r) {
for(int x : combi) System.out.print(x+" ");
System.out.println();
} else {
//DFS로 조합을 구하는 핵심 풀이
for (int i = s; i <= n; i++) {
combi[L] = i;
DFS(L + 1, i + 1);
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
r = sc.nextInt();
combi = new int[r];
DFS(0, 1);
}
}
미로 탐색

0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 0 1 1 1 0 1 1 0 0 1 0 0 0 0 0 0
풀이
이번 문제는 위에서 제시한 DFS기초 DFS 풀이 문제들을 잘 해결 했다면 쉽게 풀 수 있는 문제다.
public class 미로탐색 {
static int[] dx={-1, 0, 1, 0};
static int[] dy={0, 1, 0, -1};
static int[][] board;
static int answer=0;
public static void DFS(int x, int y){
if(x==7 && y==7) answer++;
else{
for(int i=0; i<4; i++){
int nx=x+dx[i];
int ny=y+dy[i];
//4방향으로 가게되고 해당 값이 board안에 있거나 거치치 않으면 DFS 실행
if(nx>=1 && nx<=7 && ny>=1 && ny<=7 && board[nx][ny]==0){
board[nx][ny]=1;
DFS(nx, ny);
//DFS가 끝나고 나서, 거쳐갔다는 표시 1을 0으로 바꿔 갈 수 있음을 알린다.
board[nx][ny]=0;
}
}
}
}
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
board=new int[8][8];
for(int i=1; i<=7; i++){
for(int j=1; j<=7; j++){
board[i][j]=kb.nextInt();
}
}
board[1][1]=1;
DFS(1, 1);
System.out.print(answer);
}
}섬나라 아일랜드

7
1 1 0 0 0 1 0
0 1 1 0 1 1 0
0 1 0 0 0 0 0
0 0 0 1 0 1 1
1 1 0 1 1 0 0
1 0 0 0 1 0 0
1 0 1 0 1 0 0
풀이
바로 위 문제 미로 탐색과 달리 DFS 끝나면 다시 거쳐간 표시를 없애는 것을 하지 않는다. 섬인 것을 확인했으면 계속 0으로 만들어 놓는다.
solution함수가 board를 돌면서 1이 있는 곳을 찾아내고, 해당 위치를 바탕으로 DFS를 돌려 8방향에 있는 섬을 0으로 만들어 놓는다. solution 함수가 끝나게 되면, board안에 있는 섬들의 개수를 알게 된다.
import java.util.Scanner;
public class 섬나라아일랜드 {
static int n, answer =0;
static int[][] board;
static int[] dx={-1, -1, 0, 1, 1, 1, 0, -1};
static int[] dy={0, 1, 1, 1, 0, -1, -1, -1};
public static void DFS(int x, int y) {
//해당 섬 1발견하면 모두 8방향 퍼져나가서 모두 0으로 만드는 DFS 메소드 진행
for(int i=0; i<8; i++){
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=0 && nx<n && ny>=0 && ny<n && board[nx][ny]==1){
board[nx][ny]=0;
DFS(nx, ny);
}
}
}
public static void solution() {
//board 전체를 돌며 1이 발견되는 곳을 찾아서 DFS 전달
//DFS 해당 거점으로 연결된 1을 모두 0으로 바꾼다.
//solution메소드가 끝나면 board안에 있는 모든 섬의 개수를 알게 된다.
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 1) {
board[i][j] = 0;
DFS(i,j);
answer++;
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
board = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
board[i][j] = sc.nextInt();
}
}
solution();
System.out.println(answer);
}
}피자 배달 거리(삼성 SW역량평가 기출문제 : DFS활용)

44
0 1 2 0
1 0 2 1
0 2 1 2
2 0 1 2
풀이

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class 피자배달거리 {
static class Point {
public int x, y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
static int n,m,len, answer = Integer.MAX_VALUE;
//피자집 위치를 모아놓은 pz리스트를 바탕으로 m개의 피자집을 고르는 조합의 경우를 담는 배열
static int[] combi;
//먼저 주어진 board를 다 돌면서 집과 피자집의 위치를 담아놓은 리스트
static ArrayList<Point> hs, pz;
//조합을 구하는 DFS 설명은 DFS 활용 조합 구하기편에서 볼 수 있다.
public static void DFS(int L, int s) {
if (L == m) {
//해당 조합과 집들간의 최소 위치 더한 값
//그림으로 이해 필요
int sum = 0;
for (Point h : hs) {
int dis = Integer.MAX_VALUE;
//집하나하나와 피자집 조합 4가지 위치 비교해서 가장 작은 값 구하기 =dis
for (int i : combi) {
dis = Math.min(dis, Math.abs(h.x - pz.get(i).x) + Math.abs(h.y - pz.get(i).y));
}
//그 값을 dis에 넣기
sum += dis;
}
answer = Math.min(answer, sum);
} else {
//피자집 6개 중에, 4개 조합 고르는 DFS식
for (int i = s; i < len; i++) {
combi[L] = i;
DFS(L+1, i+1);
}
}
}
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
//지도의 길이
n=kb.nextInt();
//남길 피자집의 수
m=kb.nextInt();
pz=new ArrayList<>();
hs=new ArrayList<>();
//주어진 지도를 확인하면서, pz와 hs 리스트에 위치 정보를 넣는다.
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
int tmp=kb.nextInt();
if(tmp==1) hs.add(new Point(i, j));
else if(tmp==2) pz.add(new Point(i, j));
}
}
//피자집 len개 중에 m개 조합 고르기
len=pz.size();
//m개 조합 넣을 배열
combi=new int[m];
DFS(0, 0);
System.out.println(answer);
}
}
'자바 자료구조 알고리즘 > DFS & BFS' 카테고리의 다른 글
| 코딩 테스트 Java BFS 활용 문제 풀기 (0) | 2023.05.07 |
|---|---|
| Java 그래프 문제 -인접 행렬, 인접 리스트 ,DFS, BFS (0) | 2023.05.07 |
| Java BFS 기초 이해와 문제 풀이 (0) | 2023.05.07 |
| Java DFS 기초 이해와 문제 풀이 (0) | 2023.05.07 |



