개요 목적
미래를 생각하지 않고 각 단계에서 가장 최선의 선택을 하는 기법이다.
이렇게 각 단계에서 최선의 선택을 한 것이 전체적으로도 좋은 결과를 내기를 바라는 풀이법이다.
씨름 선수

5
172 67
183 65
180 70
170 72
181 60
풀이
먼저 키가 큰 선수가 앞으로 오게 내림차순을 한다.
이제 자신 앞 선수들 중 가장 큰 몸무게보다 자신이 더 나가기만 한다면 뒤에 있는 선수들보다는 키가 크고(몸무게 비교 불필요) 앞에 있는 선수들보다는 몸무게가 많이 나가기 때문에 선발이 된다.
선발이 되면 cnt ++ 출전 선수 1명을 추가하고 가장 무거운 몸무게를 해당 선수 몸무게로 변경한다.
import java.util.*;
class Body implements Comparable<Body>{
public int h, w;
Body(int h, int w) {
this.h = h;
this.w = w;
}
@Override
public int compareTo(Body o){
return o.h-this.h;
}
}
class Main {
public int solution(ArrayList<Body> arr, int n){
int cnt=0;
Collections.sort(arr);
int max=Integer.MIN_VALUE;
for(Body ob : arr){
if(ob.w>max){
max=ob.w;
cnt++;
}
}
return cnt;
}
public static void main(String[] args){
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
ArrayList<Body> arr = new ArrayList<>();
for(int i=0; i<n; i++){
int h=kb.nextInt();
int w=kb.nextInt();
arr.add(new Body(h, w));
}
System.out.println(T.solution(arr, n));
}
}회의실 배정

5 1 4 2 3 3 5 4 6 5 7
3 3 3 1 3 2 3
풀이
가장 빨리 끝난느 회의를 찾기 위해 끝나는 시간을 기준으로 오름차순 정렬을 한다.
만약 끝나는 시간이 같다면 시작 시간으로 한번 더 오름차순 정렬한다.
회의가 가능한 회의실 끝나는 시간을 저장해 놓고
그 뒤에 오는 회의 시작 시간이 저장해 놓은 회의 끝나는 시간보다 같거나 크면 cnt++ 회의 가능 수를 추가하고, 해당 회의 끝나는 시간을 회의실 끝나느 시간으로 다시 저장해 놓는다.
import java.util.*;
class Time implements Comparable<Time>{
public int s, e;
Time(int s, int e) {
this.s = s;
this.e = e;
}
@Override
public int compareTo(Time o){
if(this.e==o.e) return this.s-o.s;
else return this.e-o.e;
}
}
class Main {
public int solution(ArrayList<Time> arr, int n){
int cnt=0;
Collections.sort(arr);
int et=0;
for(Time ob : arr){
if(ob.s>=et){
cnt++;
et=ob.e;
}
}
return cnt;
}
public static void main(String[] args){
Main T = new Main();
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
ArrayList<Time> arr = new ArrayList<>();
for(int i=0; i<n; i++){
int x=kb.nextInt();
int y=kb.nextInt();
arr.add(new Time(x, y));
}
System.out.println(T.solution(arr, n));
}
}결혼식

5 14 18 12 15 15 20 20 30 5 14
풀이

먼저 주어진 값에 시작(s)과 끝(e) 표시를 해서 내림차순으로 정렬한다. 위 오른쪽 그림을 보면, 시작일 때는 정렬 순서에 따라서 s면 cnt에 +1을 하고, e면 cnt -1을 하면 각 시간대 총 사람 수(cnt)를 구할 수 있다. cnt 중에서 가장 큰 수가 답(answer)이 되는 것이다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
public class 결혼식 {
static class Time implements Comparable<Time>{
public int time;
public char state;
Time(int time, char state) {
this.time = time;
this.state = state;
}
@Override
public int compareTo(Time ob){
if(this.time==ob.time) return this.state-ob.state;
else return this.time-ob.time;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
//시작과 종료 표시를 해서, 정렬을 한다. 위에 설명한 그림이 나올 수 있도록
ArrayList<Time> arr = new ArrayList<>();
for(int i=0; i<n; i++){
int sT=sc.nextInt();
int eT=sc.nextInt();
arr.add(new Time(sT, 's'));
arr.add(new Time(eT, 'e'));
}
Collections.sort(arr);
//s를 만나면 cnt+1 e를 만나면 cnt-1를 해서 cnt 중에서 가장 큰 값이 답(answer)이 된다.
int answer = Integer.MIN_VALUE;
int cnt = 0;
for (Time time : arr) {
if (time.state == 's') {
cnt++;
} else {
cnt--;
}
answer = Math.max(answer, cnt);
}
System.out.println(answer);
}
}
최대 수입 스케쥴(PriorityQueue 응용 문제)

6 50 2 20 1 40 2 60 3 30 3 30 1
풀이
PriorityQueue<Integer> pQ = new PriorityQueue<>(Collections.*reverseOrder*());에서 poll하면 가장 큰 값을 가져오는 것을 사용하여 코드에 적용한다.

입력 예제를 시간 순 내림 차순으로 정렬을 한다. 3일 차부터, 1일 차까지 PQ에 값을 넣어서 PQ에서 각 일마다 가장 큰 수를 answer에 더해서 결과를 산출한다. 3일 차에 넣었던 값이 2일 차 PQ에도 남아 있는 이유는 3일 이내에만 강의하면 되기 때문에 2일 차 time=3이어도 PQ에서 가장 큰 값이라면 선택 되기 때문이다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.PriorityQueue;
import java.util.Scanner;
public class 최대수입스케쥴 {
static class Lecture implements Comparable<Lecture>{
public int money;
public int time;
Lecture(int money, int time) {
this.money = money;
this.time = time;
}
@Override
public int compareTo(Lecture ob){
return ob.time-this.time;
}
@Override
public String toString() {
return "Lecture{" +
"money=" + money +
", time=" + time +
'}';
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
ArrayList<Lecture> arr = new ArrayList<>();
int max = Integer.MIN_VALUE;
for(int i=0; i<n; i++){
int m=sc.nextInt();
int d=sc.nextInt();
arr.add(new Lecture(m, d));
//가장 큰 날을 기억해 둔다. 여기서는 3
if(d>max) max=d;
}
int answer=0;
//시간 내림 차순으로 정렬
Collections.sort(arr);
//poll하면 가장 큰 값이 나올 수 있게 reversOrder를 한다.
PriorityQueue<Integer> pQ = new PriorityQueue<>(Collections.reverseOrder());
//한번 넣은 수는 다시 넣지 않도록 for문에서 분리
int k = 0;
//3일차 부터 1일차까지 PQ안에 값 중 가장 큰 값을 구한다.
for (int i = max; i >= 1; i--) {
//리스트를 탐색해서 각 일차에 맞는 값을 PQ에 넣는다.
for (; k < n; k++) {
if(arr.get(k).time<i) break;
pQ.offer(arr.get(k).money);
}
//각 일차에 PQ에서 가장 큰 값을 answer에 더한다.
if(!pQ.isEmpty()) {
Integer poll = pQ.poll();
answer+=poll;
}
}
System.out.println(answer);
}
}
다익스트라 알고리즘
다이나믹 프로그래밍을 이용한 최단 경로 찾기 알고리즘이다.
특정한 하나의 정점에서 다른 모든 정점으로 가는 최단경로를 알려준다.
단, 음의 간선이 있을 경우 사용할 수 없는 알고리즘이다.
하나의 최단 거리를 구할 때, 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다.

6 9 1 2 12 1 3 4 2 1 2 2 3 5 2 5 5 3 4 5 4 2 2 4 5 5 6 4 5
풀이
다익스트라 알고리즘 사용 조건은 가중치가 0 이상의 수(양수)여야 한다.
코드에 맞춰 그림을 더해 해당 문제 풀이 방법을 살펴보자.
먼저 이동 방향과 간선 가중치를 저장하는 graph 만들기

static ArrayList<ArrayList<Edge>> *graph*; 안에 입력값을 순회 하면서 Array 인덱스를 해당 위치로 여기고 연결 방향과 가중치 값을 담은 Edge객체를 리스트로 저장한다.
graph.get(1)은 접점 1에서 이동할 수 있는 방향과 가중치를 담은 객체를 리스트로 가진다.
만든 그래프로 다익스트라 알고리즘으로 1번 접점에서 가장 짧은 거리 구하기.
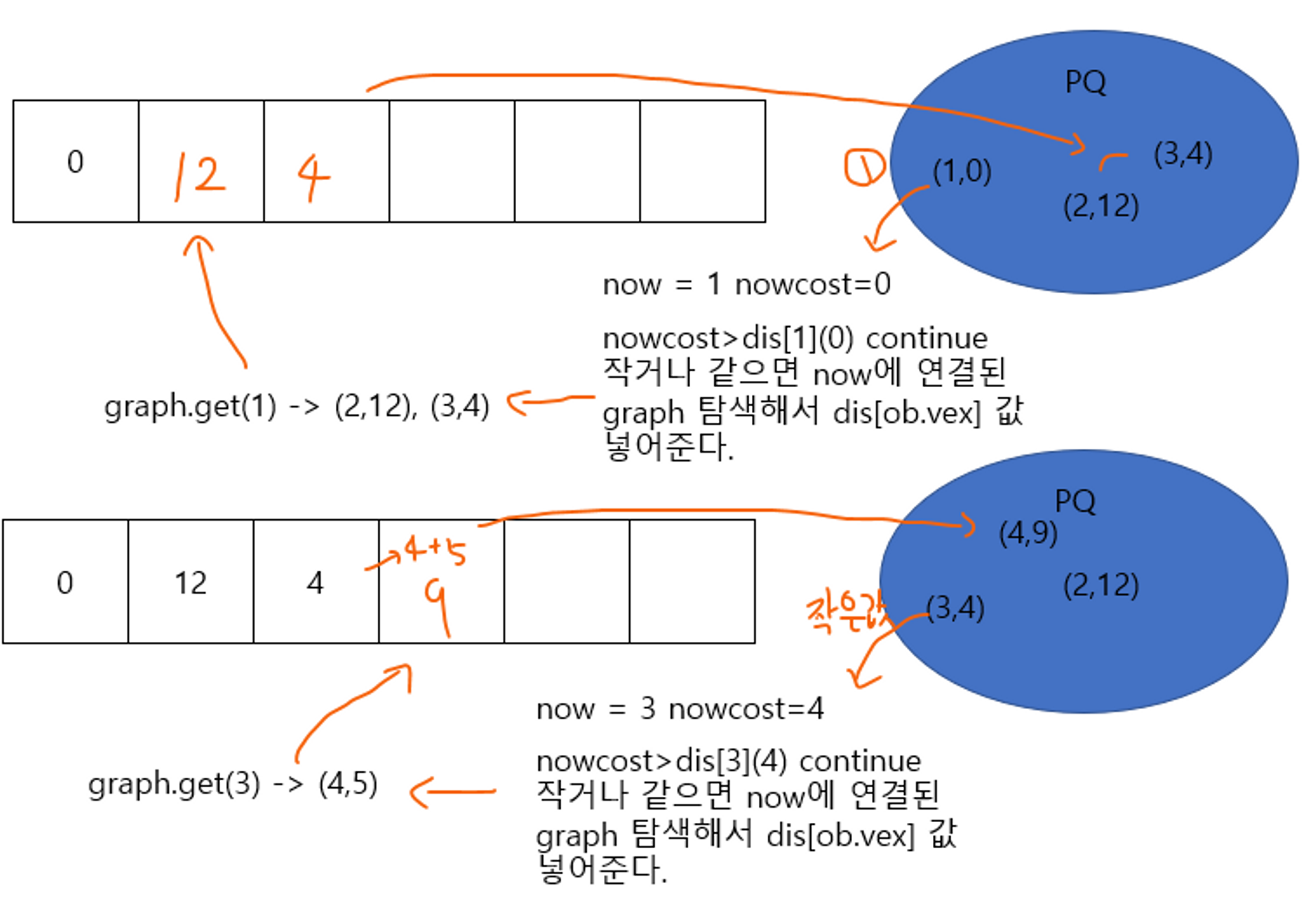
pQ에 먼저 1에서 자신으로 가는 (1,0)을 넣는다.
그리고 그에 연결된 (2,12) (3,4)의 가중치 값을 dis[1] 과 더해서 기존 dis값보다 작다면, 값을 변경하고 pQ에 값을 넣는다.
이제 pQ에서 가중치가 가장 작은 값을 꺼낸다. 이 값은 접점 1에서 가장 짧은 거리라는 것을 확신할 수 있다. 그 이후에 전에 한 행동을 반복한다.

import java.util.ArrayList;
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.Scanner;
public class 다익스트라알고리즘 {
static int n, m;
static ArrayList<ArrayList<Edge>> graph;
static int[] dis;
static class Edge implements Comparable<Edge>{
public int vex;
public int cost;
Edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
@Override
public int compareTo(Edge ob){
//우선 순위 큐에서 cost가 가장 작은 값이 나올 수 있게
// cost를 오름차순으로 정렬한다.
return this.cost-ob.cost;
}
}
public static void solution(int v){
PriorityQueue<Edge> pQ = new PriorityQueue<>();
pQ.offer(new Edge(v, 0));
dis[v]=0;
while(!pQ.isEmpty()){
Edge tmp=pQ.poll();
int now=tmp.vex;
int nowCost=tmp.cost;
if(nowCost>dis[now]) continue;
for(Edge ob : graph.get(now)){
if(dis[ob.vex]>nowCost+ob.cost){
dis[ob.vex]=nowCost+ob.cost;
pQ.offer(new Edge(ob.vex, nowCost+ob.cost));
}
}
}
}
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
n=kb.nextInt();
m=kb.nextInt();
dis=new int[n+1];
Arrays.fill(dis, Integer.MAX_VALUE);
graph = new ArrayList<ArrayList<Edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<Edge>());
}
for(int i=0; i<m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
int c=kb.nextInt();
graph.get(a).add(new Edge(b, c));
}
solution(1);
for(int i=2; i<=n; i++){
if(dis[i]!=Integer.MAX_VALUE) System.out.println(i+" : "+dis[i]);
else System.out.println(i+" : impossible");
}
}
}
친구인가?(유니온 파인드 알고리즘 활용)

9 7 1 2 2 3 3 4 1 5 6 7 7 8 8 9 3 8
풀이
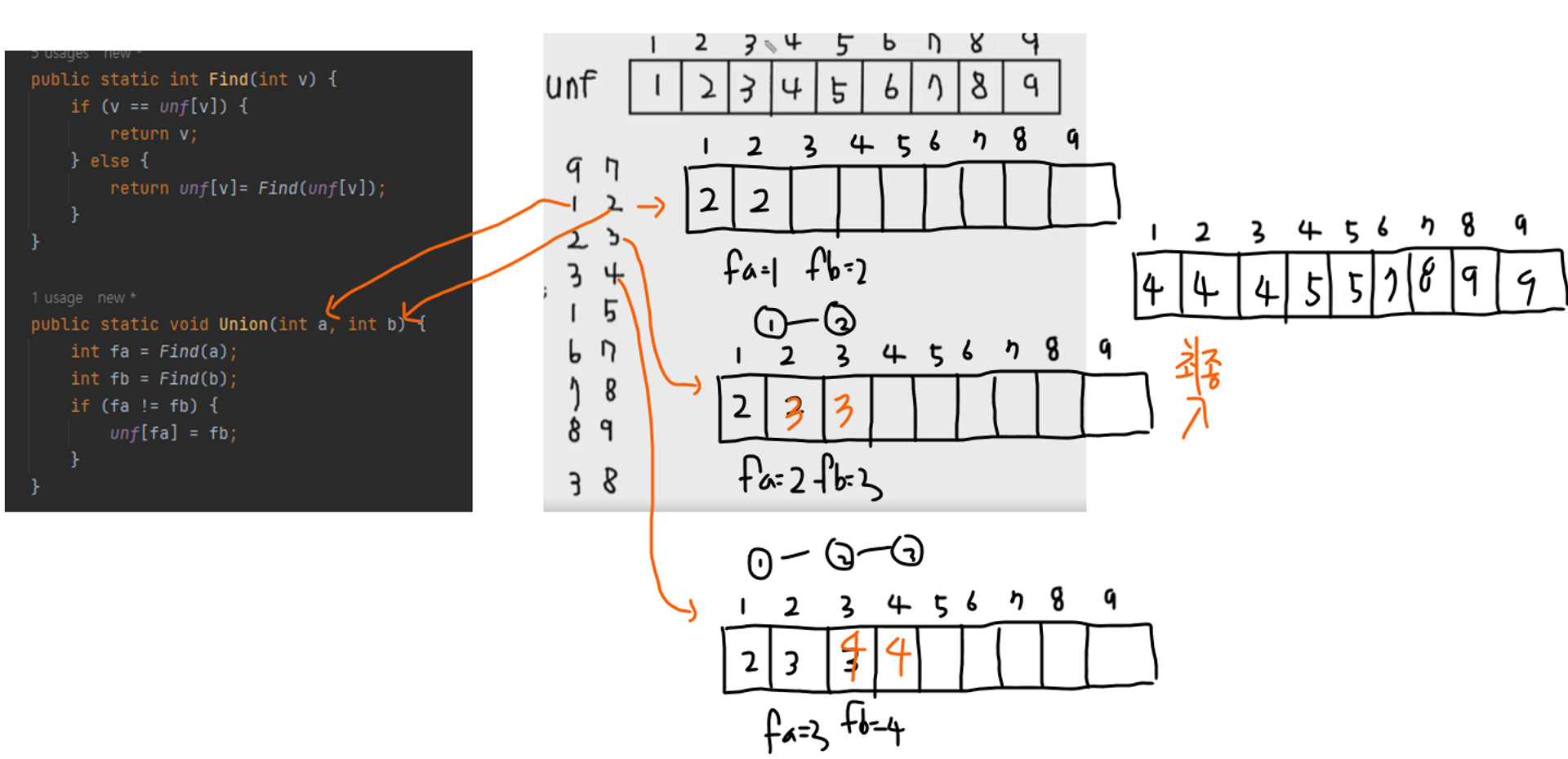
먼저 각 인덱스 번호마다 자신 인덱스와 같은 숫자를 넣어준다. 그 안에 밸류값이 같은 지에 따라서, 연결 되었는지 연결 되지 않았는지 확인을 할 것이다.

이제 Find Union을 메소드를 사용한다.
주어진 두 수는 같은 것이니깐, 두수의 밸류 값을 같게 만들어야 한다. Find 메소드로 먼저 두 값의 밸류 값을 찾는다. 그리고 유니온 메소드로 돌아와 두 값이 다르다면, unf[fa]=fb로 값을 같게 만들어 준다.
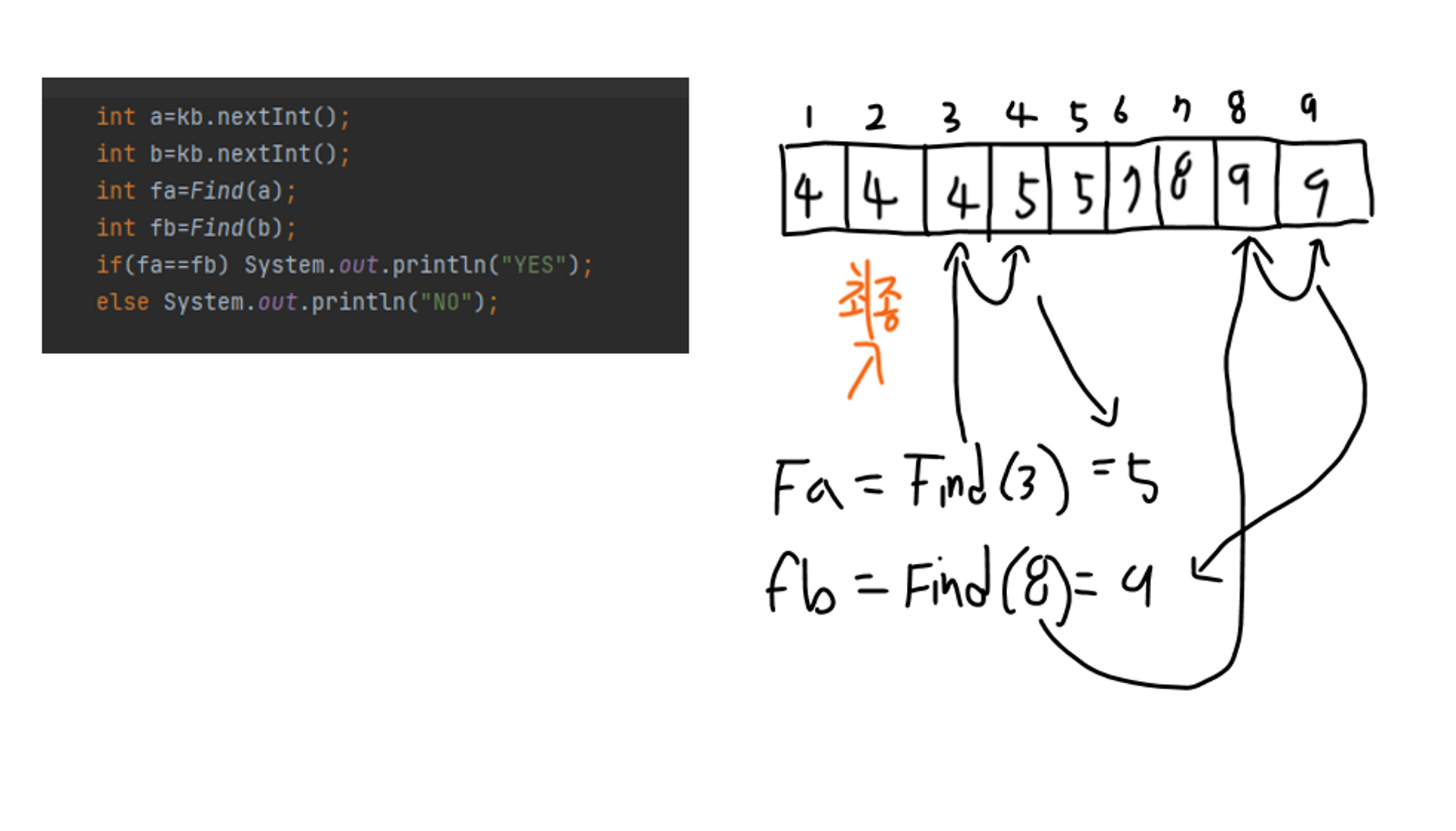
이제 마지막 3, 8 이 연결되었는 지 확인하기 위해서 Find로 각 값의 밸류값을 찾는다.
Find(3)은 3==unf[3](4)와 달라서 Find(4)→Find(5)인 =5가 나오게 되고,
Find(8)은 8==unf[8](9)와 달라서 Find(9)의 값인 = 9가 나온게 된다. 두 값이 다르기 때문에 두 수는 연결되어 있지 않다는 것을 알 수 있다.
public class 친구인가유니온파인드 {
static int[] unf;
public static int Find(int v) {
if (v == unf[v]) {
return v;
} else {
return unf[v]= Find(unf[v]);
}
}
public static void Union(int a, int b) {
int fa = Find(a);
int fb = Find(b);
if (fa != fb) {
unf[fa] = fb;
}
}
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
int n=kb.nextInt();
int m=kb.nextInt();
unf=new int[n+1];
for(int i=1; i<=n; i++) unf[i]=i;
for(int i=1; i<=m; i++){
int a=kb.nextInt();
int b=kb.nextInt();
Union(a, b);
}
int a=kb.nextInt();
int b=kb.nextInt();
int fa=Find(a);
int fb=Find(b);
if(fa==fb) System.out.println("YES");
else System.out.println("NO");
}
}
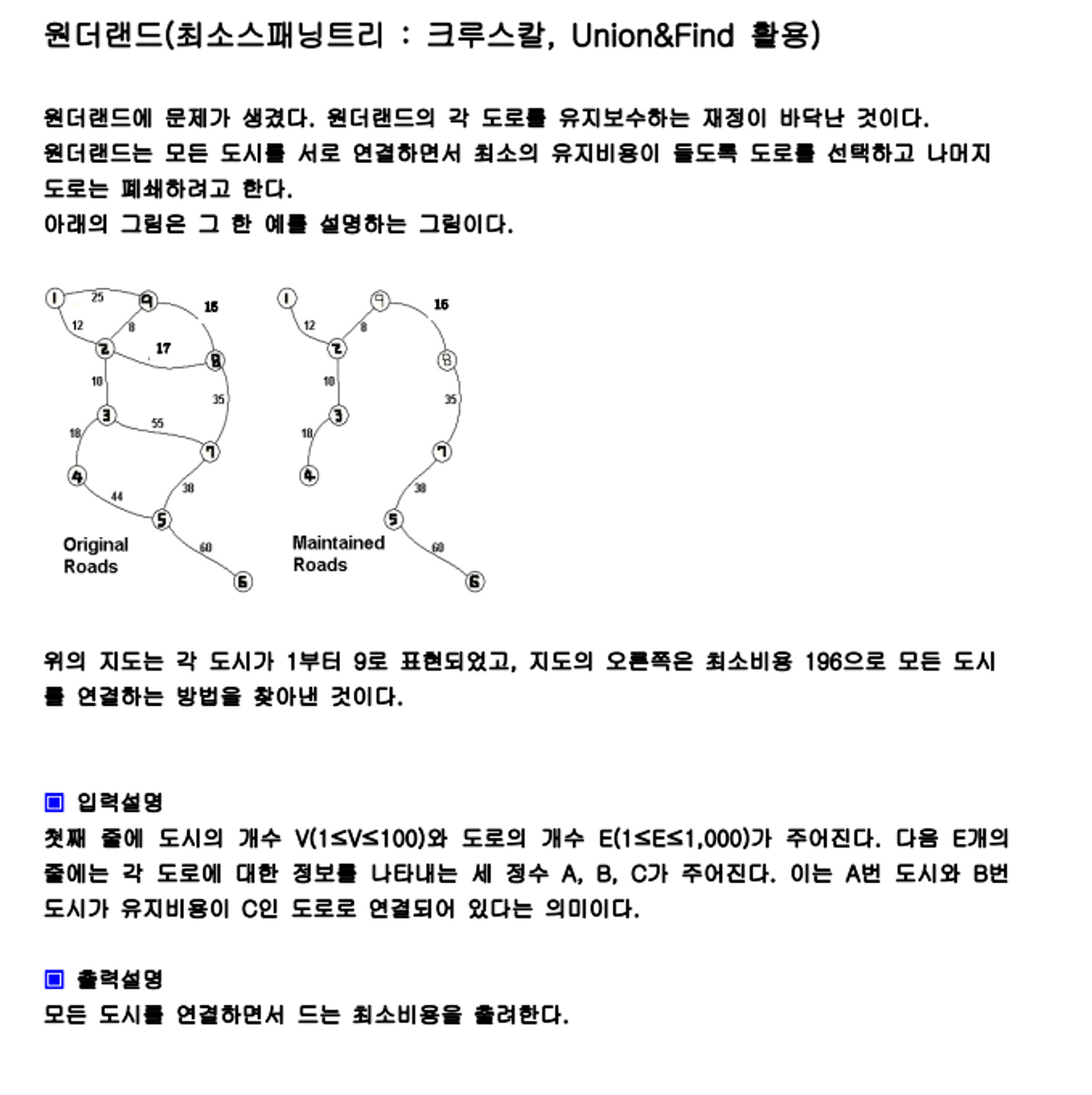
원더랜드(크루스칼 알고리즘(최소신장 트리 구하기) Union&Find 활용)
위 문제에서 활용한 Union&Find를 활용하여, 모든 정점들이 연결된 그래프의 최소 가중치 값을 구하는 방법에 대해서 알아보자.
크루스칼 알고리즘이란, 그래프 내의 모든 정점들을 가장 적은 비용으로 연결하기 위해 사용하는 알고리즘이다. 최소 신장 트리를 구하기 위한 알고리즘이다.
최소 신장 트리는 그래프에서 (1) 모든 정점을 포함하고, (2) 정점 간 서로 연결이 되며 싸이클이 존재하지 않는(tree의 기본 조건) 그래프를 의미한다.

9 12 1 2 12 1 9 25 2 3 10 2 8 17 2 9 8 3 4 18 3 7 55 4 5 44 5 6 60 5 7 38 7 8 35 8 9 15
풀이
정점과 정점 사이의 거리를 저장하는 Edge 객체를 만든다. Edge객체들을 모두 LIst에 넣은 다음에 가중치를 기준으로 오름차순으로 정렬한다. 가장 적은 값부터 연결성을 확립하기 위해서.
List에 있는 값을 하나 씩 가져와서, 둘 사이가 연결되었음을 체크하고(unf 값을 일치 시킨다) 가중치를 answer에 담는다.
그리고 만약 Uniong&Find 메소드로 이미 연결되었음을 확인하면 가중치를 더하지 않고 다음 리스트 목록으로 넘어간다.
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
public class 원더랜드 {
static class Edge implements Comparable<Edge> {
public int v1, v2, cost;
public Edge(int v1, int v2, int cost) {
this.v1 = v1;
this.v2 = v2;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
//비용 순 오름 차순이다.
return this.cost - o.cost;
}
}
public static int Find(int v) {
if (v == unf[v]) {
return unf[v];
} else {
return unf[v] = Find(unf[v]);
}
}
//a와 b를 연결시키는 메소드
public static void Union(int a, int b) {
int fa = Find(a);
int fb = Find(b);
if (fa != fb) {
//안의 밸류 값을 같게 만들어서 연결 시킴
unf[fa] = fb;
}
}
static int[] unf;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
//연결 되었는 지 확인 할 수 있는 유니온파인드 배열 인덱스별값이 같으면 연결된 것이다.
unf = new int[n + 1];
for(int i=1; i<=n; i++) unf[i]=i;
//각 점이 어떤 가중치 값으로 연결되었는 지 확인
ArrayList<Edge> arr = new ArrayList<>();
for(int i=0; i<m; i++){
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
arr.add(new Edge(a, b, c));
}
//cost 비용이 작은 순으로 정렬한다.
//그래서 작은 순으로 연결한 다음에, 연결이 안된 부분이 확인되면,
Collections.sort(arr);
int answer = 0;
for (Edge edge : arr) {
//union&find를 사용해서 연결되지 않은 점이 발견되면,
//둘을 연결시키고, 가중치를 answer에 더한다.
//그러면 최소의 가중치 값이 나온다.(cost비용을 오름차순으로 정렬 했기 때문에)
int fv1 = Find(edge.v1);
int fv2 = Find(edge.v2);
if (fv1 != fv2) {
answer += edge.cost;
Union(edge.v1, edge.v2);
}
}
System.out.println(answer);
}
}
원더랜드(최소 신장 트리 구하기 - 우선순위 큐 사용)
위와 같은 원더랜드 최소신장 트리 구하기 문제를 이번에는 우선순위 큐를 사용해서 풀어보자.
문제는 위와 같다.
풀이
어레이 리스트에 인덱스(해당 점)과 연결되어 있는, 나아갈 점과 가중치가 들어 있는 edge 객체를 리스트로 등록하자. 위 그래프를 ArrayList<ArrayList<Integer>>로 표현하면 아래와 같다.

그리고 추가로 이미 그 점을 방문 했는 지, 확인하는 ch도 점 수에 맞춰서 생성하자. ch = new int[n+1]
이제 PriorityQue를 사용해 cost가 적은 연결 점(edge)를 찾아내서, 이미 지나간 곳인지 확인하고, 지나가지 않은 곳이라면 answer에 값을 추가하고 그 점과 연결된 값들을 우선 순위 큐에 넣어서 반복한다.
<cost가 작은 순서대로 우선순위 큐 적용>
@Override
public int compareTo(edge o) {
return this.cost - o.cost;
}
--------------------------------------------------------------------------
int answer=0;
PriorityQueue<Edge> pQ = new PriorityQueue<>();
//1번 정점부터 탐색할 수 있게한다.
pQ.offer(new Edge(1, 0));
while(!pQ.isEmpty()){
//ex 1번 발견
Edge tmp=pQ.poll();
int ev=tmp.vex;
//ex 1번 지나간 곳인지 확인
if(ch[ev]==0){
ch[ev]=1;
//
answer+=tmp.cost;
//1번 거치지 않은 곳이니, 해당 graph인덱스
//1번 연결된 점들을 우선순위 큐에 다시 넣고 반복한다.
for(Edge ob : graph.get(ev)){
if(ch[ob.vex]==0) pQ.offer(new Edge(ob.vex, ob.cost));
}
//연결 된 곳 중에서 가장 비용이 작은 곳을 que에서 뽑아낸 다음
//연결된 표시가 없으면 answer에 값 추가 해당 점에서 연결된 곳 모두 q에 넣기
//이런식으로 반복한다.import java.util.ArrayList;
import java.util.PriorityQueue;
import java.util.Scanner;
public class 원더랜드우선순위큐 {
static class edge implements Comparable<edge> {
public int vex, cost;
public edge(int vex, int cost) {
this.vex = vex;
this.cost = cost;
}
@Override
public int compareTo(edge o) {
return this.cost - o.cost;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
ArrayList<ArrayList<edge>> graph = new ArrayList<ArrayList<edge>>();
for(int i=0; i<=n; i++){
graph.add(new ArrayList<edge>());
}
int[] ch=new int[n+1];
for(int i=0; i<m; i++){
int a=sc.nextInt();
int b=sc.nextInt();
int c=sc.nextInt();
graph.get(a).add(new edge(b, c));
graph.get(b).add(new edge(a, c));
}
int answer=0;
PriorityQueue<edge> pQ = new PriorityQueue<>();
pQ.offer(new edge(1, 0));
while(!pQ.isEmpty()){
edge tmp=pQ.poll();
int ev=tmp.vex;
if(ch[ev]==0){
ch[ev]=1;
answer+=tmp.cost;
for(edge ob : graph.get(ev)){
if(ch[ob.vex]==0) pQ.offer(new edge(ob.vex, ob.cost));
}
}
}
System.out.println(answer);
}
}